| |
| |
| Wir wollen nun einen Algorithmus kennen lernen, mit dessen Hilfe sozusagen rein "mechanisch" die Gültigkeit einer Formel überprüft werden kann. Der Resolutionskalkül dient dabei, neben der Methode der Wahrheitstafeln der Aussagenlogik sowie den rein syntaktischen Deduktionskalkülen der Aussagen- und Prädikatenlogik, als weiteres syntaktisches Entscheidungsverfahren für die Frage nach der Gültigkeit logischer Ausdrücke. Die Aufgabe des Resolutionskalküls besteht konkret darin, die Unerfüllbarkeit (Kontradiktion) einer gegebenen Formelmenge nachzuweisen. Der Resolutionskalkül hat die Eigenschaft der Korrektheit (Widerspruchsfreiheit), indem er keine erfüllbare Formel als vermeintlich unerfüllbar deklariert. Er ist darüber hinaus insofern vollständig, als er jede unerfüllbare Formel als solche nachweist. Mit Hilfe der Resolution werden v. a. zwei Fragestellungen abgehandelt:
|
| |
||||
| Definition 5.1.1 Ein Literal ist eine atomare Formel oder deren Negation. Voraussetzung für die aussagenlogische Resolution ist, dass die betrachtete Formel in KNF vorliegt. Dabei werden Formeln in KNF für die Zwecke der Resolution in der sog. Klauselform notiert. Aus
erhält man die Klauselform
Jedes Element von F heißt Klausel
und besteht ausschließlich aus Literalen, die
allesamt Disjunktionsglieder sind. Die Klauseln selbst
sind Konjunktionsglieder. Wegen der Mengennotation sind
die Formeln (( p1 Definition 5.1.2 Seien K1,
K2 Klauseln. Dann heißt
R Resolvent von K1 und K2,
falls es ein Literal L gibt mit L
wobei gilt:
Resolvent und zugehörige Klauseln können leicht als Diagramm veranschaulicht werden. Anmerkung 5.1.1 Aus letzterer Definition
geht hervor, dass auch die leere Menge als Resolvent auftreten
kann. Diese wird mit dem speziellen Symbol Satz 5.1.1 (Resolutionslemma) Sei
F eine Formel in KNF, dargestellt als Klauselmenge. Ferner
sei R ein Resolvent zweier Klauseln K1,
K2 in F. Dann sind F und F
Beweis: (1) Falls || F (2) Sei umgekehrt || F || = 1 iff für alle
K
Beispiel 5.1.1 Die Klauselmenge {{ p3,
¬ p4, p1
}, { p4, ¬ p1
}} hat die beiden Resolventen { p3,
p1, ¬ p1
} sowie { p3, p4,
¬ p4 }. Die Klauselmenge {{
p1 }, { ¬ p1
}} hat genau einen Resolventen: Die leere Menge, die wir
im Zusammenhang der Resolution mit Definition 5.1.3 Sei F eine Klauselmenge. Dann ist Res ( F ) definiert als
Ferner gilt: Der entscheidende Satz für die aussagenlogische Resolution lautet nun: Satz 5.1.2 Eine Klauselmenge F ist
unerfüllbar genau dann, wenn Beweis: Wir wollen hier nur kurz die
Korrektheit der Resolution betrachten: Die leere Klausel
Wenn Definition 5.1.4 Eine Deduktion der leeren Klausel aus einer Klauselmenge F ist eine Folge K1, K2, ..., Km von Klauseln mit der Eigenschaft:
Anmerkung 5.1.2 Eine Klauselmenge ist also genau dann unerfüllbar, falls die leere Klausel aus ihr deduziert werden kann. Die selbe Klausel kann innerhalb des Deduktionsprozesses in mehreren Resolutionsschritten verwendet werden. Der Aufwand einer solchen Deduktion kann, ebenso wie beim Verfahren der Wahrheitstafeln, exponentiell sein, das heißt die Deduktion der leeren Formel kann zu exponentiell vielen Formeln führen. Aus diesem Grunde ist das Resolutionsverfahren nicht per se "effizienter" als die Methode der Wahrheitstafeln. Beispiel 5.1.2 Sei F = {{ ¬ p, q }, { ¬ q }, { p }} eine Klauselmenge. Wir deduzieren dann:
|
| |
| In der Prädikatenlogik kann nicht unmittelbar der Resolvent zweier Klauseln { P ( f ( a )) } und P ( x ) bestimmt werden, da beide Klauseln zwar genau die selben Prädikate enthalten, diese jedoch unterschiedlich prädizieren. Wir bedürfen zu aller erst des "Gleichnamigmachens" beider Klauseln, etwa dadurch, dass in der zweiten Klausel x durch f ( a ) ersetzt wird. Diese Art der Substitution nennt man Unifikation in der PL. Wir hätten auch zuerst x durch f ( y ) und dann y durch a ersetzen können, nur wäre diese Substitutionskette "länger", sozusagen "komplexer". Ferner sehen wir, wie wichtig es ist, dass die "unifizierten" Ausdrücke allquantorfizierte Variablen enthalten. Definition 5.2.1 Eine Substitution sub heißt Unifikator einer Menge von Literalen L = { L1, L2, ..., Lk }, falls L1 sub = L2 sub = ... = Lk sub. Das heißt durch Anwendung der Substitution auf jedes Literal von L entsteht ein und dasselbe Literal. Man schreibt hierfür auch | L sub | = 1 und sagt L sei unifizierbar. Ein Unifikator sub einer Literalmenge L heißt allgemeinster Unifikator von L, falls für jeden Unifikator sub' von L gilt, dass es eine Substitution s gibt, so dass sub' = sub s ist (dieser Ausdruck besagt, dass für jedes Literal gilt Li sub' = Li sub s). Anmerkung 5.2.1 Der allgemeinste Unifikator kann algorithmisch hergeleitet werden:
Anmerkung 5.2.2 In jedem Schleifendurchlauf ersetzt letzterer Algorithmus, fall es nicht infolge der Stopp-Bedingung terminiert, eine Variable x, die nach Ausführung der Substitution also nicht mehr in der Literalmenge L vorkommt. Es können also höchstens so viele Schleifendurchläufe auftreten, wie zu Beginn verschiedene Variablen in L vorhanden sind.
Definition 5.2.2 Die Nichtübereinstimmungsmenge D ( L ) einer Menge von Literalen ist die Menge aller Teilformeln bzw. Terme von Elementen von L, die jeweils an der selben Stelle innerhalb von Literalen (Atome oder deren Negation) von L am weitesten links vorkommen und jeweils mit verschiedenen Symbolen beginnen. L besteht dabei nur aus Literalen, die aus identischen Prädikaten aufgebaut sind. Beispiel 5.2.1 Sei die Literalmenge
gegeben.
Unser allgemeinster Unifikator hat also die Gestalt:
Definition 5.2.3 (Prädikatenlogische Resolution) Seien K1, K2 und R prädikatenlogische Klauseln. Dann ist R ein prädikatenlogischer Resolvent von K1, K2, falls gilt:
Anmerkung 5.2.3 Die erste Bedingung letzterer Definition benötigen wir, damit wir mit der zweiten Stopp-Bedingung des Unifikationsalgorithmus keine Schwierigkeiten bekommen. Arbiträre Variablenbezeichner sollen der Resolution nicht im Wege stehen. Ferner ist eine solche Umbenennung wegen Satz 4.5.1 zulässig. Die Definition der Menge L in der zweiten Definitionsbedingung ist vor dem Hintergrund zu verstehen, dass die Literale unifizierbar sein müssen, also als identische Zeichenketten auftreten müssen. Wir bemerken ferner, dass die aussagenlogische Resolution einen Spezialfall der prädikatenlogischen Resolution darstellt, insofern als für diese s1 = s2 = [ ] sowie m = n = 1 gilt. Es gilt nun wieder, was hier nicht eigens formal eingeführt
werden muss, dass eine Klauselmenge dann unerfüllbar
ist, falls sie die leere Klausel Satz 5.2.1 Sei F eine Formel in SNF
mit der Matrix F' in KNF. Dann gilt: F ist unerfüllbar
genau dann, wenn Anmerkung 5.2.4 Für eine Menge
prädikatenlogischer Formeln P kann nun die Formel P
|
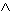 ...
... 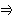 q iff
q iff  { 1, ..., n }: pi
{ 1, ..., n }: pi
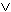 ... Ln11
)
... Ln11
) 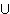 ( K2
- {
( K2
- {  } )
} )
 gekennzeichnet. Eine Klauselmenge, die
gekennzeichnet. Eine Klauselmenge, die