|
|
─quivalenzklassen 
|
|
|
Behauptung: Sei R  A
x A eine Äquivalenzrelation über A2
und sei a A
x A eine Äquivalenzrelation über A2
und sei a  A. Dann heißt
| a | def= { b | < a,
b > A. Dann heißt
| a | def= { b | < a,
b >  R } Äquivalenzklasse
von a und für alle c R } Äquivalenzklasse
von a und für alle c  A gilt dann: Entweder | c | = | a
| (falls < c, a >
A gilt dann: Entweder | c | = | a
| (falls < c, a >  R) oder | c | ∩ | a | =
R) oder | c | ∩ | a | = 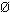 .
Darüber hinaus ist die Vereinigung aller Äquivalenzklassen
äquivalent zu A. .
Darüber hinaus ist die Vereinigung aller Äquivalenzklassen
äquivalent zu A.
Beweis: Zunächst stellen wir fest, dass,
da R eine Menge ist, entweder < a, c >  R oder < a, c >
R oder < a, c > 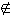 R. Wir haben also
zwei Fälle zu unterscheiden: R. Wir haben also
zwei Fälle zu unterscheiden:
1. Sei < a, c >
 R (also gilt auch, da R
symmetrisch ist, < c, a > R (also gilt auch, da R
symmetrisch ist, < c, a >  R). Sei nun b
R). Sei nun b  | a
| ein beliebiges (!) Element aus | a | iff < a,
b > | a
| ein beliebiges (!) Element aus | a | iff < a,
b >  R und < b,
a > R und < b,
a >  R. Dann gilt
aber, da R transitiv ist, < b, c
> R. Dann gilt
aber, da R transitiv ist, < b, c
>  R und < c,
b > R und < c,
b >  R, insgesamt
also: b R, insgesamt
also: b  | c |. Genau
die gleiche Überlegung kann für beliebige Elemente
d | c |. Genau
die gleiche Überlegung kann für beliebige Elemente
d  | c | angestellt
werden. Also gilt unter genannter Voraussetzung (da R
zudem reflexiv ist) | a | = | c |. | c | angestellt
werden. Also gilt unter genannter Voraussetzung (da R
zudem reflexiv ist) | a | = | c |.
2. Sei nun < a, c >
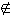 R. Angenommen nun, | a
| ∩ | c | ≠ { }. Es existiere nun (im Widerspruch
zur Behauptung) ein b, mit b R. Angenommen nun, | a
| ∩ | c | ≠ { }. Es existiere nun (im Widerspruch
zur Behauptung) ein b, mit b  | a | und b
| a | und b  | c
|. Dann gilt aber: < a, b > | c
|. Dann gilt aber: < a, b >  R und < b, c >
R und < b, c >  R. Wegen der Transitivität von R folgt
dann im Widerspruch zur Annahme, dass < a,
c >
R. Wegen der Transitivität von R folgt
dann im Widerspruch zur Annahme, dass < a,
c >  R. Also gilt unter
genannter Voraussetzung: | a | ∩ | c
| = { }. R. Also gilt unter
genannter Voraussetzung: | a | ∩ | c
| = { }.
Ferner ist die Vereinigung aller Äquivalenzklassen äquivalent
zum Universum A, denn zu jedem Element aus A existiert genau
eine Äquivalenzklasse (da R reflexiv ist).
|
Anmerkungen
zu Satz 2.2.2 
|
|
|
Der Satz 2.2.2 soll hier nicht bewiesen werden. Um Teil
(1) des Satzes zu beweisen, zeigt man, dass mit a
≤ b iff a  b = a eine Ordnungsrelation gegeben ist,
das heißt dass ≤ unter den genannten Bedingungen
reflexiv, antisymmetrisch und transitiv ist. Für
die Reflexivität haben wir also etwa zu zeigen, dass
in Verbänden stets die Beziehung a
b = a eine Ordnungsrelation gegeben ist,
das heißt dass ≤ unter den genannten Bedingungen
reflexiv, antisymmetrisch und transitiv ist. Für
die Reflexivität haben wir also etwa zu zeigen, dass
in Verbänden stets die Beziehung a  a = a gilt. Dies folgt unmittelbar mit
Hilfe der Absorptionsgesetze (und der Kommutativität),
denn
a = a gilt. Dies folgt unmittelbar mit
Hilfe der Absorptionsgesetze (und der Kommutativität),
denn
(( a  b )
b )  a )
a )  a = a iff
a = a iff
a
 a
= a, daraus folgt: a
= a, daraus folgt:
a
≤ a
Das heißt ich ersetze den geklammerten Ausdruck
gemäß Absorptionsgesetz (ganz analog zeigt
man, dass a  a = a). Da wir nun aber wissen, dass
unter den gemachten Voraussetzungen stets b ≤
b für beliebige b gilt, wissen
wir zugleich, dass a
a = a). Da wir nun aber wissen, dass
unter den gemachten Voraussetzungen stets b ≤
b für beliebige b gilt, wissen
wir zugleich, dass a  b = a iff a
b = a iff a  b = b, denn: (1) sei a
b = b, denn: (1) sei a  b = a, dann gilt: ( a
b = a, dann gilt: ( a  b )
b )  b = b iff a
b = b iff a  b = b. (2) gelte umgekehrt a
b = b. (2) gelte umgekehrt a
 b
= a, dann gilt: ( a b
= a, dann gilt: ( a
 b
) b
)  a = a iff b a = a iff b
 a
= a iff a a
= a iff a  b = a. Wegen der Reflexivität von
≤ folgt aus a ≤ b weiterhin: inf
( a, b ) = a und sup ( a,
b ) = b, womit auch die Existenz von
Infimum und Supremium "gezeigt" wäre.
b = a. Wegen der Reflexivität von
≤ folgt aus a ≤ b weiterhin: inf
( a, b ) = a und sup ( a,
b ) = b, womit auch die Existenz von
Infimum und Supremium "gezeigt" wäre.
Der zweite Teilsatz wird dadurch bewiesen, dass man die
Eigenschaften der Kommutativität, Assoziativität
und Absorption für sup und inf aufzeigt.
Auf diesen Überlegungen aufbauend, können wir
einfach folgern, dass in Booleschen Algebren folgendes
gilt: a 
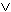 a = a = 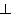 und a
und a 
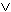 a = a =  .
Denn die dritte definitorische Eigenschaft legt für
Boolesche Algebren gerade fest, dass stets die Beziehungen
( a .
Denn die dritte definitorische Eigenschaft legt für
Boolesche Algebren gerade fest, dass stets die Beziehungen
( a 
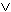 a ) a )  b = b und ( a
b = b und ( a 
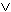 a ) a )  b = b gelten. Also gilt auf Grundlage
von Satz 2.2.2 für die verbandsgeordnete Menge, die
der betrachteten Booleschen Algebra entspricht (Boolesche
Algebren sind Verbände mit bestimmten Eigenschaften!):
b ≤ a
b = b gelten. Also gilt auf Grundlage
von Satz 2.2.2 für die verbandsgeordnete Menge, die
der betrachteten Booleschen Algebra entspricht (Boolesche
Algebren sind Verbände mit bestimmten Eigenschaften!):
b ≤ a 
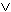 a und a a und a 
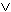 a ≤ b für
alle b des betrachteten Universums. ZurŘck
zu Satz 2.2.2 a ≤ b für
alle b des betrachteten Universums. ZurŘck
zu Satz 2.2.2
|
|
 A
x A eine Äquivalenzrelation über A2
und sei a
A
x A eine Äquivalenzrelation über A2
und sei a  A. Dann heißt
| a | def= { b | < a,
b >
A. Dann heißt
| a | def= { b | < a,
b > 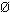 .
Darüber hinaus ist die Vereinigung aller Äquivalenzklassen
äquivalent zu A.
.
Darüber hinaus ist die Vereinigung aller Äquivalenzklassen
äquivalent zu A. 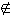 R. Wir haben also
zwei Fälle zu unterscheiden:
R. Wir haben also
zwei Fälle zu unterscheiden: a = a iff b
a = a iff b
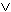 a =
a =