| |
|||
| Jede mathematische Theorie beginnt mit der Definition ihrer
primitiven Einheiten, aus denen sie ihre zusammengesetzten Einheiten
aufbaut. Die Logik basiert u. a. auf der Mengentheorie. Unsere
primitiven Einheiten sind somit Mengen, Objekte, die
wir mit a, b, c, ... bezeichnen wollen.,
sowie die Relation Î, die als "ist
enthalten in" zu lesen ist. Als Menge, symbolisiert durch
Großbuchstaben, werden Aufsammlungen von Objekten bezeichnet,
die Elemente dieser Mengen heißen. Wir schreiben
a Das mathematische Mengenkonzept ist infolge unserer alltäglichen Erfahrungen unmittelbar einsichtig: "Wir müssen es als eine grundlegende Fähigkeit des menschlichen Geistes ansehen, gegebene Objekte gedanklich zu einem Ganzen zusammenfassen zu können." (Heuser 1990:17). Dieser exemplifizierende Bezug ist in der Logik sicher nicht immer möglich, woran wir erkennen, dass Logik eine formale, mathematische Disziplin ist. Dieser Bezug ergibt sich allerdings dort, wo die Logik als Repräsentationssprache (etwa in der Sprachwissenschaft) Verwendung findet. Wir unterscheiden die folgenden, aus der Mengenlehre wohl bekannten Symbole: "a " " "=def" steht für "wird definiert durch" (bisweilen verwenden wir auch die Schreibweise "=") "{a | P}" steht für "die Menge aller Entitäten mit der Eigenschaft P" Andere Symbole werden ja nach Bedarf eingeführt. Definition 2.1.1 Es gelten folgende Beziehungen zwischen Mengen, hierbei sei U das betrachtete Universum (i. e. die Menge aller betrachteten Objekte): 1. 2. A 3. A = B iff A 4. Das Kreuzprodukt: A x B
=def { < a, b > | a
5. Die Vereinigung: A 6. Der Durchschnitt: A
∩ B =def { a 7. Die Differenz: A - B
= def { a 8. Die Summe: A + B =def
( A 9. Das Komplement von A: Ac
=def {a Anmerkung 2.1.1 Die Mengen A und B heißen
disjunkt iff A ∩ B =
entsprechend steht ∩i=1,...,nvAi
für A1 Anmerkung 2.1.2 Zum Kreuzprodukt (auch:
Cartesisches Produkt): Sei M eine Teilmenge eines Cartesischen
Produktes zweier Mengen. Dann kann man nach den kleinsten Teilmengen
A, B dieser Mengen fragen, so dass A x B = M.
Hierzu definiert man: A = { a | < a, b
> Beispiel 2.1.1 Seien A = { a, c, d } und B = { b, d, e }zwei Mengen über dem Universum U = { a, b, c, ..., z }. Dann gilt: 1. A x B = { < a, b >, < a, d >, < a, e >, < c, b >, < c, d >, < c, e >, < d, b >, < d, d >, < d, e > }. 2. A ∩ B = { d }. 3. A 4. A + B { a, c, b, e }. 5. A - B = { a, c }. 6. Ac = U - A. Definition 2.1.2 < a, b > =def {{ a }, {a, b }} ist das geordnete Paar der Elemente a, b. Anmerkung 2.1.3 < a, b > definiert eindeutig eine Ordnung der Elemente der Menge { a, b }. Daher ist < a, b > ≠ < b, a >, da {{ a }, {{a, b }} ≠ { a }, {{ a, b }} (vorausgesetzt a ≠ b). In der Mengentheorie gelten folgende grundlegende Gesetze: 1. Idempotenz: A 2. Kommutativität: A 3. Assoziativität: A 4. Distributivität: A 5. Identitätsgesetze: A 6. Komplementgesetze: A 7. De Morgansche Gesetze: ( A 8. Konsistenzprinzip: A Definition 2.1.3 R heißt n-stellige
Relation über A1, ..., An
iff R Definition 2.1.4 Sei R 1. reflexiv iff für alle a
2. irreflexiv iff für alle a 3. symmetrisch iff < a,
b > 4. antisymmetrisch iff ( < a,
b > 5. asymmmetrisch iff < a,
b > 6. transitiv iff ( < a,
b > 7. linear iff < a, b
> 8. Äquivalenzrelation iff R ist reflexiv, symmetrisch und transitiv. 9. Ordnungsrelation iff R ist reflexiv, antisymmetrisch und transitiv. 10. Toleranzrelation iff R ist reflexiv und symmetrisch. Sei R Definition 2.1.5 Sei R eine Relation.
Die kleinste transitive Relation R' Definition 2.1.6 Eine Relation F
Für Funktionen F schreibt man auch F : A
Definition 2.1.7 Eine Funktion F
: A 1. partiell iff es gibt mindestens ein
a 2. total iff für alle a 3. injektiv iff ( F (
a ) = F ( b )) 4. surjektiv iff für jedes b
5. bijektiv iff F ist injektiv und surjektiv. Beispiel 2.1.2 Sei A die Menge aller
europäischen Hauptstädte, N die Menge
der natürlichen Zahlen, F : A 1. F ist eine Funktion: Jede Hauptstadt hat eine bestimmt Zahl von Einwohnern (und nicht etwa mehrere Einwohnerzahlen). 2. F ist total: Es gibt keine Hauptstadt ohne Einwohner. 3. F ist nicht injektiv: Mehrere Hauptstädte können die gleiche Zahl von Einwohnern aufweisen. 4. F ist nicht surjektiv: Z. B. gibt es keine Hauptstad mit 1 Mrd. Einwohnern. 5. R ist reflexiv: Jede Hauptstadt hat so viele Einwohner wie sie selbst. 6. R ist symmetrisch: Falls a so viele Einwohner hat wie b, dann gilt auch das Umgekehrte. 7. R ist transitiv: Falls a so viele Einwohner hat wie b, das so viele Einwohner hat wie c, dann haben a und c die gleiche Anzahl von Einwohnern. 8. R ist folglich eine Äquivalenzrelation: Mit Hilfe von R kann die Menge aller europäischen Hauptstädte in Äquivalenzklassen von Städten mit gleicher Einwohnerzahl geteilt werden. Die Vereinigung dieser Äquivalenzklassen entspricht A. 9. Q ist eine Toleranzrelation. Definition 2.1.8 Das Komplement einer
Relation R
Definition 2.1.9 Die Inverse R-1einer Relation R ist definiert als
Definition 2.1.10 Definition2.1.11 Seien f : A
Definition 2.1.12 Die Funktion idA
: A Definition 2.1.13 BA =
{ f | f : A Definition 2.1.14 Die Menge aller Teilmengen von A heißt Potenzmenge von A und wir mit Pot ( A ) symbolisiert. |
| |
| Definiton 2.2.1 Für jede natürliche
Zahl n Definition 2.2.2 Sei F eine Menge
von Operationen beliebiger Stelligkeit über der Menge
A. Definition 2.2.3 Eine Algebra A ist ein Tupel < A, f1, ..., fn, c1, ..., ck>, für das gilt: 1. Die Menge A heißt Universum von A. 2. f1, ...,
fn sind Operationen
über A, das heißt fi : Asi 3. ci,
..., ck Anmerkung 2.2.1 Als Algebren gelten somit Entitäten von zunächst "allgemeiner Natur": Die wichtigste Festlegung besteht darin, dass eine Menge vorliegt, über der eine oder mehrere Funktionen definiert sind, deren Wertebereich wieder Teilmenge der Ausgangsmenge ist. Eine Algebra formalisiert also eine Menge zusammen mit Operationen auf dieser Menge, die angeben, wie man mit den Elementen dieser Menge "rechnen" kann. Definition 2.2.4 Der Typ einer Algebra
A = < A, f1,
..., fn, ...> ist ein geordnetes
Paar ( F, σ ), wobei F =
{ f1, ..., fn
} und σ : F Definition 2.2.5 Zwei Algebren A, B sind von demselben Typ, falls die in ihnen definierten Operationen paarweise die selbe Stelligkeit haben, das heißt die i-te Operation fi aus A hat die selbe Stelligkeit wie die i-te Operation gi aus B. Beispiel 2.2.1 Sei Beispiel 2.2.2 Ist < Definition 2.2.6 Seien A,
B Algebren desselben Typs mit den Universen
A, B. Eine Abbildung h : A
n ist die Anzahl von Operationen der Algebren A und B. si ist die Stelligkeit der i-ten Operation fiA aus A bzw. fiB aus B. Beispiel 2.2.3 Sei A
= < A, ... > eine Algebra und idA
die Identitätsabbildung auf A. Ist dann idA
: A Anmerkung 2.2.2 Falls h : A
Beispiel 2.2.4: Sei A
= < Homomorphismen sollen nun mit Hilfe von Graphen veranschaulicht werden. Das hat den Vorteil, dass die Struktur von Graphen gewissermaßen "visualisiert" werden kann. Graphen sind aber keine Algebren, da die Relation der Kanten eines Graphen keine Relation darstellt. Wir müssen also zunächst Graphen gesondert definieren: Definition 2.2.7 Sei V eine nicht-leere
Menge. Sei ferner E Definition 2.2.8 Seien G1
= < V1, E1
>, G2 = < V2,
E2 zwei Graphen. φ
: G1
Beispiel 2.2.5 Seien A = { 1,
2, 3, 4 } und B = { F, S, Q
} zwei Mengen. Es gelte nun G1 =
< A, {( 1, 4 ), ( 1, 2 ), ( 2, 2 ), ( 2, 3 )}>
sowie G2 = < B, {( S,
Q ), (S, F ), ( F, F
)}>. G1, G2
sind Graphen und es kann ein Homomorphismus h :
G1 Definition 2.2.9 Seien A,
B zwei Algebren desselben Typs und sei
h ein Homomorphismus von A nach B.
Dann heißt h Isomorphismus von A nach B, falls h eine
bijektive Abbildung ist. A, B
heißen dann isomorph, und man schreibt
hierfür A Anmerkung 2.2.3 Liegt ein Isomorphismus zwischen zwei Algebren vor, so kann die eine Algebra aus der anderen sozusagen durch Umbenennungen gewonnen werden. Anmerkung 2.2.4 Falls A
= < A1, f1,
..., fn > eine Algebra mit n
verschiedenen Operationen ist, so kann A
der Einfachheit halber auch mittels < A,
F > wiedergegeben werden,
wobei F = { f1,
..., fn }. Ferner: Wenn
A = < A, f1,
..., fn > eine Algebra mit endlich
vielen Operationen ist, dann notiert man den Typ dieser
Algebra auch in der Form ( σ1,
..., σn ), wobei σi
die Stelligkeit der Operation fi
ist für i Anmerkung 2.2.5 Was soll man vor dem
Hintergrund der in 2.2.1 gegebenen Definition für Operationen
unter einer nullstelligen Operation verstehen? Man kann
An als die Menge aller Abbildungen g
: { 0, 1, ..., n - 1 } Unter diesen Voraussetzungen ist dann A0
= { g | g : An = { g | g : {
0, ..., n - 1 } Es ist üblich, auf der Basis vorhandener mathematischer Strukturen neue Strukturen abzuleiten bzw. zu entwickeln. Im Bereich der allgemeinen Algebra kann dies mit Hilfe sogenannter Subalgebren (Auch Unteralgebren genannt) geschehen. Der Vorteil abgeleiteter Strukturen besteht darin, dass ihre Eigenschaften durch Bezug auf bzw. Einschränkung von (strukturellen) Eigenschaften bereits bekannter Strukturen definierbar sind. Definition 2.2.10 Sei A =
< A, f1A,
..., fnA > eine
Algebra vom Typ ( F, σ ). Sie ferner
B
heißt dann Subalgebra von A,
wobei fiB : Bni
Es gilt weiterhin: σ ( f1B ) = σ ( f1A ) = ni. Falls B eine Subalgebra von A ist, dann schreibt man B ≤ A. Die Menge aller Universen von Subalgebren einer Algebra A ist Sub ( A ) = { B | B = < B, F > ≤ A }. Eine Teilmenge B Beispiel 2.2.6 Sei die Algebra
N = < Wir wollen an dieser Stelle eine einfache Eigenschaft von Subalgebren beweisen, um ein wenig Gespür für diesen Vorgang zu gewinnen. Natürlichsprachlich formuliert lautet der zu beweisende Satz: Das System der Subalgebren einer Algebra ist unter der Durchschnittsbildung ( das heißt unter der Operation " ∩ " abgeschlossen. Mathematisch formuliert wird hieraus: Satz 2.2.1 Sei A
= < A, F
> eine Algebra mit Operationen f
Beweis: Teilsatz (1) folgt unmittelbar
aus der Definition für Subalgorithmen: Es gilt für
alle Algebren A = < A,
F > : A ≤ A.
Und daher: A Sei nun f Natürlich kann für das Beweisen von mathematischen Sätzen kein "Rezept" (das heißt Algorithmus) angegeben werden, so dass die Befolgung des Algorithmus den gesuchten Beweis automatisch herzuleiten gestattet. Mathematische Beweise stellen vielmehr komplexe Gebilde dar, zu deren Herleitung bisweilen ein Höchstmaß an Kreativität erforderlich ist. In unserem Fall reicht es allerdings aus, Satz und Definition der durch den Beweis betroffenen Entitäten "genau zu studieren". Jeder Schritt des Beweises ist dann eine unmittelbare Folgerung aus den Behauptungen des Satzes, den Festlegungen der entsprechenden Definitionen und/oder aber eine Folgerung aus aus einem vorangehenden Beweisschritt, für den die selbe Überlegung angestellt werden kann. Definition: 2.2.11 Ein Verband ist
eine Algebra V = < V, Anstelle von Verbänden können wir auch folgende, einfacher definierte Struktur betrachten: Definition 2.2.12 Eine verbandsgeordnete
Menge ist ein Tupel < V, ≤ >,
das heißt eine Struktur aus einer Menge und einer
Ordnungsrelation ≤
inf und sub können auch auf Teilmengen
von V bezogen werden: Sei A Beispiel 2.2.7 Sei I = [ 0, 1
] das Einheitsintervall, das heißt die Menge aller
realen Zahlen, die größer-gleich 0 bzw. kleiner-gleich
1 sind. ≤ sie die bekannte Relation über der Menge
der realen Zahlen, wobei < a, b >
Zwischen verbandsgeordneten Mengen und Verbänden besteht folgender Zusammenhang: Satz 2.2.2 (1) Wenn V
= < V, Wir sind nun in der Lage die für die klassische Logik so fundamentale Struktur der Booleschen Algebren einzuführen: Definition 2.2.13 Eine Boolesche Algebra
ist eine Algebra < A,
Anmerkung 2.2.6 Die dritte Bedingung
der Definition für Boolesche Algebren impliziert die
Existenz von Anmerkung 2.2.7 Die Aristotelische
Logik beansprucht u. a. die Geltung des Gesetzes vom ausgeschlossenen
Drittel (ungefähr so: "Eine beliebige Aussage
ist wahr oder falsch, ein Drittes gibt es nicht.")
sowie diejenige des Gesetzes vom ausgeschlossenen Wiederspruch
("Eine beliebige Aussage ist nicht gleichzeitig wahr
oder falsch."). In ihrer algebraischen Notation (auf
der Grundlage Boolescher Algebren) können diese beiden
Gesetze mittels a Bevor wir einige Beispiele Boolescher Algebren kennen lernen werden, soll zunächst noch eine wichtige Eigenschaft dieser Klasse von Algebren bewiesen werden, nämlich die Idempotenz: Satz 2.2.3 Sei A
= < A, Beweis: Wir wollen nur die Eigenschaft
a Dieser Beweis zeigt gerade, dass unabhängig davon, welche Boolesche Algebra man auch vorliegen haben mag, von der Geltung der Idempotenz ihrer beiden fundamentalen zweistelligen Operationen ausgegangen werden kann, da diese allgemein für alle Booleschen Algebren gilt: Die Eigenschaft der Idempotenz wurde für die Klasse der Booleschen bewiesen und gilt nunmehr für jede ihrer Instanzen. Beispiel 2.2.8 Sei U eine beliebige
Menge, dann ist PU = < Pot ( U
), Beispiel 2.2.9 Sei ΞA
= { Xx | X
Eine Boolesche Algebra und man kann einen Homomorphismus
h : PA
Beispiel 2.2.10 Sei die Algebra
|
| |
|||||
| Definition 2.3.1 Ein Monoid ist eine
Algebra < A, ο, ε >
mit der Signatur ( 2, 0 ), die folgende Gleichungen
für alle a, b, c
Beispiel 2.3.1 Sei die Algebra < Definition 2.3.2 Sei A eine beliebige
Menge und sei con eine Funktion mit con ( a, b ) = a
b (die "Hintereinanderschreibung" von a und b) für
alle a, b Definition 2.3.3 Sei A eine beliebige Menge. Sei z. B. A eine Menge von Symbolen. Es kann nun mit Hilfe von con ein Monoid F ( A ) = < A*, con, ε > konstruiert werden, welches als das durch A determinierte freie Monoid bezeichnet wird. A* heißt Kleene-Hülle von A und wird wie folgt definiert:
Man hat dann:
Die Menge A wird auch als Alphabet bezeichnet. A* ist die Menge aller endlichen Strings aus Elementen der Menge A. Beispiel 2.3.2 Sei A die Menge
der Buchstaben des deutschen Alphabets. Dann gilt etwa:
Computerlinguistik Das rekursive Konstruktionsprinzip, welches der Ableitung der Kleene-Hülle zugrunde liegt, kann als ein grundlegendes Prinzip (unter anderen) zum Aufbau der Syntax formaler Sprachen verstanden werden. Natürlich schränkt man bei der Bildung formaler Sprachen die Menge syntaktisch wohlgeformter Ausdrücke durch Angabe zusätzlicher Bildungsregeln ein. Das rekursive Konstruktionsmuster werden wir aber vielfach erhalten geblieben sehen.
|
|
|
 A,
falls a Element der Menge A ist, andernfalls schreiben wir
a
A,
falls a Element der Menge A ist, andernfalls schreiben wir
a 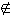 A.
A. 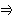 "
steht für "daraus folgt, dass"
"
steht für "daraus folgt, dass"
 " bzw. "iff" steht
für "genau dann, wenn"
" bzw. "iff" steht
für "genau dann, wenn" 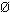 = {} ist die
leere Menge, also die Menge, die keine Elemente enthält.
= {} ist die
leere Menge, also die Menge, die keine Elemente enthält. B
iff ( a
B
iff ( a 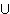 B =def { < ).
B =def { < ).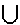
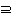 heißt transitive Hülle von R.
heißt transitive Hülle von R.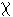 A
:
A
: 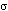 : F
: F 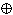 , 0 >, mit a
, 0 >, mit a
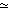 B.
B.
 ( b
( b  > ein Verband ist, und ≤
> ein Verband ist, und ≤ 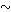 > mit den
Zusatzbedingungen:
> mit den
Zusatzbedingungen:
 und
und 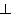 ,
nämlich:
,
nämlich:  ,
,
 ,
, 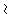 > mit:
> mit: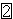 ist eine Boolesche Algebra.
ist eine Boolesche Algebra.