| |
| Die Formalisierung der Logik hat die Konstruktion einer formalen Sprache zum Ziel, mit deren Hilfe jene Struktureigenschaften von Schlüssen exakt formalisiert werden solllen, die ihre Gültigkeit oder Falschheit bedingen. In Analogie zur linguistischen Analyse natürlicher Sprachen besteht die Konstruktion einer formalen Sprache aus der Angabe einer Syntax sowie einer Semantik: Die Syntax einer formalen Sprache ist ein Regelsystem, das Bildungsregeln für die wohlgeformten Ausdrücke dieser Sprache beschreibt. Die Semantik einer solchen Sprache weist jedem ihrer Ausdrücke eine Bedeutung zu, d. h. einen Ausdruck einer formalen Sprache, welche die Semantik der betrachteten Sprache formalisiert. Die Zuweisung einer Bedeutung zu einem zusammengesetzten Ausdruck vollzieht sich folgendermaßen: "The meaning of a complex expression is a function of the meanings of its parts and of the syntactic rules by which they are combined." (Partee et al. 1990:318) Dieses Prinzip wird rekursiv auf die Bedeutungen der Teilausdrücke angewandt, bis man an den atomaren Ausdrücken anlangt. Dieses Vorgehen einer funktionalen Ableitung der Bedeutung eines komplexen Ausdrucks aus den Bedeutungen seiner Teilausdrücke beruht auf dem sogenannten Kompositionalitätsprinzip der Bedeutung, das Frege zugeschrieben wird, der es aber nicht explizit erwähnt. Wenn nun aber die Logik die Formalisierung von Schlüssen zum Ziel hat, die wir mit Hilfe natürlicher Sprachen ausdrücken, so muss die Logik gerade von jenen Operationen Gebrauch machen, die sie zu formalisieren beabsichtigt. Wenn wir nämlich die Logik als formale Sprache konstruieren bzw. definieren, so geschieht dies mit Hilfe einer natürlichen Sprache, z. B. mit Hilfe des Deutschen. Wie kann dieser scheinbare Widerspruch aufgelöst werden? Die Lösung des Problems stammt von Taski (siehe Tarski 1977), der zwei Sprachebenen unterscheidet: Die Objektsprache als Ebene der formalen Logik wird mit Hilfe einer Metasprache, die sozusagen auf einer Ebene oberhalb der Objektsprache liegt, eingeführt. Als Metasprache dient uns im folgenden das Deutsche. Treten in einem metasprachlichen Ausdruck objektsprachliche Termini auf, die zugleich Elemente der Metasprache sind, so werden diese mittels " ‘‘ " und " ’’ " besonders gekennzeichnet. So wird etwa mit einem ‘‘und’’ ein objektsprachliches Zeichen markiert. Bereits bei der Einführung in die Mengenlehre haben wir gesehen, dass beim Aufbau einer formalen Sprache zunächst ihre primitiven oder auch atomaren Einheiten, aus denen sich alle anderen Ausdrücke dieser Sprache zusammen der Sprache zusammensetzen, einzuführen sind. Die Wahl der primitiven Einheiten restringiert selbstverständlich die Ausdrucksstärke der konstruierten Sprache. Die Aristotelische Logik benannte Begriffe, Urteile und Schlüsse als die atomaren Einheiten der Logik. Diese Dreiteilung der Grundbegriffe der Logik wurde im wesentlichen durch das Mittelalter hindurch bis heute beibehalten. Ein Satz ist eine Rede, die etwas von etwas bejaht oder verneint. Sie entweder allgemein oder partikulär oder unbestimmt. Allgemein nenne ich sie, wenn etwas jedem oder keine zukommt, partikulär, wenn es irgend einem oder irgend einem nicht oder nicht jedem zukommt, unbestimmt, wenn die Rede etwas zukommen oder nicht zukommen lässt ohne den Zusatz allgemein oder partikulär (so dass sie es unbestimmt lässt, in welcher von beiden Weisen es zu nehmen ist), wie z. B. in dem Satz: Das Konträre fällt unter die selbe Wissenschaft, oder: Die Lust ist kein Gut. [...] Begriff [...] nenne ich die Bestandteile, in die der Satz als in Prädikat und Subjekt der Prädikation sich auflöst, mag nun das Sein bei der Bejahung hinzugesetzt oder bei der Verneinung, wo es Nichtsein wird, ausgeschieden werden. Ein Schluss ist eine Rede, in der, wenn etwas gesetzt wird, etwas von dem Gesetzten Verschiedenes notwendig dadurch folgt, dass dieses ist. Mit dem Ausdruck: Dadurch, dass dieses ist, meine ich, dass die Folge seinetwegen eintritt, und damit, dass sie seinetwegen eintritt, dass es sonst keines, von außen zu nehmenden Begriffs bedarf, damit sich ihre Notwendigkeit ergibt. Vollkommen nenne ich einen Schluss, der, damit seine Notwendigkeit einleuchtet, außer den Voraussetzungen keiner weiteren Bestimmung bedarf, unvollkommen eine solchen, der noch einer oder mehrerer weiterer Bestimmungen bedarf, die zwar wegen der zugrunde liegenden Begriffe notwendig gelten, aber nicht in den Vordersätzen enthalten sind. Von George Boole (1815 - 1864) und Augustus De Morgan (1806 - 1871) stammt die für die formale Logik grundlegende algebraische Behandlung der klassischen Logik: Begriffe und Sätze (Urteile) wurden durch Variablen ersetzt sowie Schlüsse durch algebraische Operationen beschrieben. Friedrich Ludwig Gottlob Frege (1848 - 1925) entwickelte die Idee der Formalisierung der Logik via Kalkül weiter. Seine primitiven Einheiten sind Gedanken, die entweder wahr oder falsch sein können. Bertrand Russell (1870 - 1972) und Alfred N. Whitehead (1861 - 1947) nannten ihre primitiven Einheiten Propositionen, die das umfassen, was ein Aussagesatz ausdrückt. Propositionen sind Äquivalenzklassen der Relation "Der Satz Si hat dieselbe Bedeutung wie der Satz Sj". Propositionen, die keine anderen Propositionen enthalten, heißen atomar. Atomare Propositionen sind die logischen Atome der Aussagenlogik. Die "Wörter" der Aussagenlogik sind durch Variablen, die atomare Propositionen symbolisieren, sowie durch eine Reihe logischer Symbole gegeben. Definition 3.1.1 Sei ATOM = { p,
q, r, ... } die Menge der atomaren bzw.
elementaren Propositionen. Sei ferner SYMB = { Die Menge aller möglichen "Strings" über LPROP ist L*PROP. Eine echte Teilmenge dieser Menge (das heißt das Universum des durch LPROP determinierten freien Monoids enthält die syntaktisch wohlgeformten Ausdrücke der propositionalen Logik, die Formeln genannt werden. Definition 3.1.2 Die Menge der wohlgeformten
Formeln der Aussagenlogik der Aussagenlogik ist die kleinste Menge
PROP
Die Konstruktion einer wohlgeformten Formel kann mit Hilfe eines Baumes dargestellt werden, der als Blätter die atomaren Propositionen und als Wurzel den zusammengesetzten Ausdruck ausweist. Beispiel 3.1.1 Ein Konstruktionsbaum für
( q
Definition 3.1.3 Auf der Grundlage der Operationen
Man liest " p Der Aufbau der Aussagenlogik ist durch die Angabe von Syntaxregeln natürlich nicht beendet. Der Aufbau einer Logik erfolgt vielmehr durch Angabe eines Kalküls, der ein Alphabet, eine Menge von Axiomen sowie eine Menge von Ableitungs- oder Deduktionsregeln als Komponenten enthält. Ein Kalkül verfolgt den Zweck, mit Hilfe der Axiome unter Verwendung der Deduktionsregeln Formeln aus PROP abzuleiten, die Sätze oder Theoreme genannt werden. Die Grundidee des Kalküls besteht also darin, Formeln als Theoreme aus einer gegebenen Menge von Axiomen abzuleiten, die als "wahr" betrachtet werden, und zwar unter Absehung der Bedeutungen der in den Sätzen auftretenden Aussagen. Die Ableitung der Theoreme erfolgt sozusagen rein syntaktisch, ohne Referenz auf die Semantik der verwendeten elementaren Aussagen. Man kann daher einen Kalkül auch als ein Verfahren betrachten, mit dessen Hilfe die Theoreme einer Sprache systematisch aufgezählt werden können, ohne dass der Kalkül zugleich entscheidbar zu sein braucht. Der erste Kalkül für die Aussagen- und Prädikatenlogik stammt von B. Russell und A. N. Whitehead (1910). Von Hilbert stammt der Versuch, die gesamte Mathematik mit Hilfe eines Kalküls zu formalisieren:
Ein Kalkül der Aussagenlogik wäre also gegeben durch
eine Teilmenge von PROP, den Axiomen, sowie durch eine Menge von
Ableitungsregeln, die Operationen der Form PROP x PROP Als notwendige und hinreichende Voraussetzungen für das Funktionieren eines Kalküls nennt Hilbert folgende Bedingungen:
|
| |
| Definition 3.2.1 Die Menge AXIOM der Axiome der Aussagenlogik enthält die folgenden Formeln aus PROP:
Definition 3.2.2 Es existiert genau eine Deduktionsregel: Man nennt diese Regel modus ponens (MP). Anmerkung 3.2.1 Der MP ist eine Regel,
die einen Schluss von den zwei Prämissen p und p
Entscheidend ist nur, dass die Einsetzung für p
und q konsistent vorgenommen wird und dass q und q Definition 3.2.3 Sei P " Definition 3.2.4 p* =def
{ q | p
Definition 3.2.5 Sei P
Definition 3.2.6 p heißt
Theorem iff Beispiel 3.2.1 Es gilt: ( p Satz 3.2.1 Deduktionstheorem: { p
} Beweis: Wir haben zwei Schritte zu beweisen:
Anmerkung 3.2.2 Das Deduktionstheorem ist ein sogenanntes Metatheorem. Ein Metatheorem ist kein Theorem der Aussagenlogik, sondern über die Aussagenlogik. Das Deduktionstheorem beschreibt eine abstrakte Beziehung, die zwischen bestimmten Schlüssen der Aussagenlogik gilt. Satz 3.2.2 Sei ≈ Beweis:
Definition 3.2.7 sei PROP≈
die Menge der Äquivalenzklassen gemäß
der Relation ≈. Ferner gelte für beliebige
| p |, | q |
< PROP≈, ≤ > ist dann eine
verbandsgeordnete Menge, < PROP≈,
Satz 3.2.3 | p | | q | = inf ( | p |, | q | ). Beweis: Nach Axiom (7) gilt
Anmerkung 3.2.3 Der hier vorgestellte Kalkül für die Aussagenlogik entspricht nicht der Hilbertschen Forderung nach Einfachheit. Man kann Kalküle für die Aussagenlogik konstruieren, die mit erheblich weniger Axiomen auskommen. Hier ein Beispiel: Die Menge AXIOM enthalte folgende Axiome:
Als Ableitungsregel fungiert wieder der MP. Wir können
dann z. B. die Beziehung AXIOM
|
| |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Definition 3.3.1 Die Semantik der Aussagenlogik
wird erklärt mittels einer Funktion || || : PROP
Anmerkung 3.3.1 Wir bemerken, dass die Funktion || || insbesondere für die Formel p 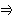 q festlegt, dass
q festlegt, dass
Gilt nun in jedem Falle || p || = 0,
so folgt hieraus, dass die Implikation || p Die Bedeutung einer wohlgeformten Formel p resultiert aus der Anwendung von || || auf p. Die Bedeutung einer zusammengesetzten Formel ist eine Funktion der Bedeutungen der atomaren Formeln, welche durch die Blätter des Konstruktionsbaumes für p dargestellt werden. Hinter dieser Festlegung verbirgt sich ein rekursives Prinzip: Die Bedeutung eines Ausdrucks der Aussagenlogik ist eine Funktion der Bedeutungen seiner unmittelbaren Teilausdrücke, deren Bedeutungen wiederum auf der Basis desselben Prinzips bestimmt werden. Dieses Kompositionalitätsprinzip der Bedeutung haben wir weiter oben bereits kennen gelernt. Natürliche Sprachen "verletzen" dieses Prinzip in aller Regel: Die Bestimmung der Bedeutungen natürlichsprachlicher Äußerungen eruiert die Einbeziehung ihrer ko- und kontextuellen Einbettung. Die Zuordnung von Wahrheitswerten zu den atomaren Propositionen heißt Interpretation oder auch Belegung. Die Frage, ob eine beliebige wohlgeformte Formel p
Definition 3.3.2 Seien p, q
Beispiel 3.3.2 Es gilt:
Anmerkung 3.3.2 Die de Morganschen Gesetze legen es nahe, die Semantik sämtlicher bisher eingeführter aussagenlogischer Funktoren allein mit Hilfe der Negation und Implikation zu definieren. So gilt etwa:
Dass diese Äquivalenzen unmittelbar auf den syntaktischen
Ableitungsoperator " " übertragbar sind,
folgt aus dem Vollständigkeitssatz (s. u.). Das heißt
aber, dass die Semantik der Aussagenlogik vollständig mit
Hilfe der beiden Funktoren "¬" und " Definition 3.3.3 Eine Belegung der Formeln
aus PROP heißen Bewertung, wenn für alle
p, q
Anmerkung 3.3.3 Neben den bislang eingeführten Funktoren existiert noch eine Reihe anderer zweistelliger Funktoren (genau 24 = 16 verschiedene Funktoren, da genau 16 verschiedene vierstellige Permutationen der Elemente 0, 1 mit Wiederholung und Berücksichtigung der Reihenfolge existieren). Hier ist ihre vollständige Liste:
Beispiel 3.3.2 p
Beispiel 3.3.4 Der semantische Ableitungsoperator
"
" Definition 3.3.5 Cons ( p
) =def { q | p Wir wollen an dieser Stelle die Widerspruchsfreiheit und Vollständigkeit das eingeführten Aussagenkalküls beweisen. Satz 3.3.1 Widerspruchsfreiheit: Alle auf der Grundlage der Menge AXIOM und des MP beweisbaren Sätze sind Tautologien. Vollständigkeit: Alle Tautologien sind auf der Grundlage der Menge AXIOM und des MP beweisbar. Mit anderen Worten:
Beweis: Zunächst zur Widerspruchsfreiheit:
Alle Axiome p Beweisidee Nun
zur Vollständigkeit: Wir erinnern uns, dass eine Menge
M von Formeln konsistent heißt, falls die Beziehung
M
Wird die Geltung dieser drei Sätze einmal vorausgesetzt, so kann die Vollständigkeit des Aussagenkalküls folgendermaßen (indirekt) gezeigt werden: Ist p nicht im Aussagenkalkül beweisbar, so ist nach Satz (1) die Menge { ¬ p } konsistent. Nach Satz (2) und (3) existiert dann eine Menge M* mit einer Bewertung, die die Sätze von M* erfüllt, also insbesondere ¬ p. Dann ist aber p aussagenlogisch falsch. Also gilt: Wenn p nicht im Aussagenkalkül beweisbar ist, dann ist p aussagenlogisch falsch. Wir wollen nun (der Übung halber) zumindest die ersten beiden Hilfssätze beweisen:
Wir können diesem Vollständigkeitssatz ein grundlegendes Aufbauprinzip formaler Sprachen, wie etwa der Aussagenlogik, entnehmen, nämlich dass die Sätze einer solchen Sprache gerade so aufgebaut sind, dass ihre syntaktische Struktur ihrer semantischen Struktur entspricht, wobei syntaktische Regeln für das Schließen angegeben werden, die den inhaltlichen Folgerungsbeziehungen entsprechen.
|
| |
| Definition 3.4.1 Eine wohlgeformte Formel ist in konjunktiver Normalform (KNF) bzw. in disjunktiver Normalform (DNF) iff sie von der Form
(bzw. von der Form ( P1 Satz 3.4.1 Zu jeder wohlgeformten Formel
p Wir wollen diesen Satz an dieser Stelle nicht beweisen, sondern vielmehr einen Algorithmus zur Ableitung der KNF (bzw. DNF) einer beliebigen Formel angeben:
Beispiel 3.4.1 Überführung von
( p
|
|
|
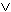 ,
,
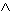 (, ), ¬,
(, ), ¬,  )} die Menge der Symbole. Das Alphabet der propositionalen
Logik ist dann die Menge LPROP = ATOM
)} die Menge der Symbole. Das Alphabet der propositionalen
Logik ist dann die Menge LPROP = ATOM 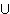 SYMB.
SYMB. L*PROP,
für die gilt:
L*PROP,
für die gilt: PROP folgt: ( p
PROP folgt: ( p 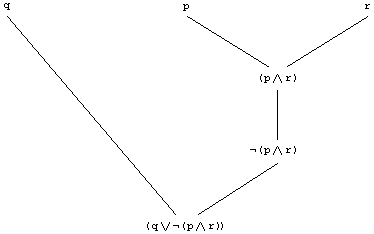
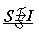
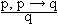
 q. Oftmals schreibt man anstelle
von " P
q. Oftmals schreibt man anstelle
von " P 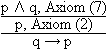
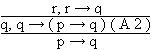
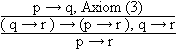
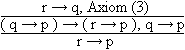

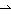
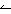
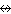
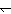

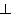
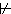 p,
dann ist die Menge { ¬ p } konstant.
p,
dann ist die Menge { ¬ p } konstant.