| |
| Die Prädikatenlogik ist eine Erweiterung der Aussagenlogik in dem Sinne, als sie anstelle elementarer Aussagenvariablen nunmehr strukturierte Ausdrücke betrachtet. Aus der Aussagenlogik wissen wir bereits, wie ein logisches System einzuführen ist. Dieses wird in drei Schritten aufgebaut: Die Syntax legt fest, welches zulässige Ausdrücke der Sprache sind. Die Semantik bestimmt die Interpretationen der Ausdrücke, schließlich ist in einem abschließenden Schritt die Widerspruchsfreiheit und Vollständigkeit des Systems nachzuweisen. Wir wollen uns der Prädikatenlogik zunächst informell nähern. Wir erinnern uns, dass Aristoteles elementare Aussagesätze als Ausdrücke bezeichnet hat, in denen etwas (mit Hilfe des Prädikats) von etwas (dem Subjekt) ausgesagt wird. Da auf der Stufe der Prädikatenlogik deiktische Ausdrücke (wie etwa Pronomina, Orts- und Zeitadverbien) nicht betrachtet werden, können wir zunächst (informell) das logische Prädikat durch denjenigen Teil des Satzes bezeichnet sehen, den man erhält, falls man den Subjektnamen (und eventuell auftretende Objektnamen) herausstreicht, als z. B. "Logik macht Spaß." oder " Trier liegt an der Mosel." Durch Herausstreichen von Subjekts- und Objektnamen erhält man Leerstellen im Satz, die als Bestandteile der Prädikate betrachtet werden. Ein Prädikat mit n Leerstellen wird als n-stelliges Prädikat bezeichnet. Eine Art Normalform für Prädikate erreichen wir, falls der Prädikatsname vorangestellt erscheint. Aus unseren Beispielen wir also: "macht Spaß (Logik)" sowie "liegt an (Trier, Mosel)". Natürlich ist die Reihenfolge der geklammerten Ausdrücke bedeutsam. In einem letzten Schritt werden die "sprechenden" Namen unserer prädikatenlogischen Ausdrücke durch Variablen und / oder spezielle Ausdrücke für Konstanten ersetzt, als etwa " P ( a ) " oder " G ( b, c ) ". Damit haben wir eine erste, rudimentäre Formalisierung der Struktur einfacher Aussagesätze erreicht. Die Leerstelle eines Prädikats, in welche die Konstanten eingesetzt werden, können durch Ausdrücke für Variablen markiert werden: Etwa " P ( x ) ". Für die Variable können dann Konstanten eingesetzt werden, um den Ausdruck wieder "eindeutig" zu machen. Die Bedeutung eines Prädikats ist eine Relation über dem betrachteten Universum, einstellige Prädikate bedeuten Eigenschaften.Die Erweiterung der Ausdrucksstärke der Prädikatenlogik
gegenüber der Aussagenlogik besteht nun im wesentlichen
in der Einführung prädikatenlogischer Operatoren,
die aus einstelligen Prädikaten (wahrheitsfunktionale)
Sätze erzeugen. Hierzu existieren die Quantoren "
∀ " (Allquantor) und " ∃ " (Existenzquantor).
Sei Wir können nun einige natürlichsprachliche Sätze versuchsweise prädikatenlogisch formalisieren:
Betrachten wir den Satz "Jemand liebt jeden" (prädikatenlogisch
"
Die Umkehrung dieses Schlusses gilt sicherlich nicht. Allerdings gilt jedoch die generelle Vertauschbarkeit von identischen Quantoren, so z. B.:
Und selbstverständlich gilt, dass wenn nur eine Entität des Universums die Eigenschaft F besitzt, dann nicht alle Entitäten die Eigenschaft F nicht besitzen, also:
M. a. W.: Der Existenzquantor kann mit Hilfe des Allquantors definiert werden. |
| |
| Das Alphabet der Prädikatenlogik (PL) ist
die Vereinigung der Mengen PSYMB = { Für Konstanten und Variablen werden wir immer metasprachliche
Ausdrücke a, b, c, ...,
P, G, F, ... bzw. x,
y, z, ... verwenden. Unsere Objektsprache
ist die Sprache der Prädikatenlogik, unsere Metasprache
ist das Deutsche. Ein Ausdruck der Art " F
( x ) Wir verwenden weiterhin das metasprachliche Symbol " * ", zu dem es keine objektsprachliche Entsprechung gibt. Ist " A [ * ] " irgend eine endliche Folge von Grundzeichen der Sprache PL und " * ", so ist " A [ B ] derjenige Ausdruck aus PL, der entsteht, falls alle Vorkommnisse von " * " in " A [ * ] " durch B ersetzt werden. Wir definieren nun, was ein wohlgeformter Ausdruck der Sprache PL ist: Definition 4.2.1 Die Menge TERM wird wie folgt definiert:
Definition 4.2.2 Die Menge der atomaren Formeln ATOM ist definiert durch:
Definition 4.2.3 Die Menge PRAED der wohlgeformten Formeln der Prädikatenlogik ist definiert durch:
Ferner legen wir fest, dass äußere Klammern
immer weggelassen werden können. Zwischen den Funktoren
besteht folgende Bindungsordnung (bei abnehmender Bindung):
¬, Definition 4.2.4 Es gilt:
Definition 4.2.5 Die Menge FV der
freien Variablen einer wohlgeformten Formel p
Beispiel 4.2.1 FV ( Definition 4.2.6 Eine Formel p
Wir wollen an dieser Stelle zunächst die Semantik und dann erst syntaktische Ableitungen innerhalb der Prädikatenlogik betrachten. Diese Vorgehensweise empfiehlt sich, da der Ableitungsbegriff in der Prädikatenlogik um einiges komplizierter ist als in der Aussagenlogik. Die Semantik der Prädikatenlogik bietet aber ein leicht zu vermittelndes Verständnis der grundlegenden Konstrukte dieser formalen Sprache.
|
| |
|||||
| Die Semantik der PL wird mit Hilfe einer
Interpretationsfunktion || || eingeführt, die eine
Interpretation der prädikatenlogischen Terme, Funktionen
und Relationen über einem Gegenstandsbereich U,
den wir Universum nennen wollen, umfasst. Die Gegenstandskonstanten
bezeichnen Objekte (Entitäten oder auch Einheiten)
aus U, Prädikatskonstanten stehen für
Begriffe, deren Umfänge mengentheoretisch über
Teilmengen von Elementen aus Der Umfang eines einstelligen Begriffs (i. e. einer Eigenschaft)
umfasst alle Objekte aus U, die diese Eigenschaft
haben. Der Umfang einer n-stelligen Relation ist
gleich der Menge aller n-stelligen Folgen von Objekten,
die in dieser Relation zueinander stehen. Eine Interpretation
der PL über dem Universum U ist dann erklärt
über eine Funktion || ||, die jeder Gegenstandskonstanten
a ein Objekt || a || Beispiel 4.3.1 Sei U = Anmerkung 4.3.1 Wie kann nun ein quantifizierter
Satz der Art " ∀ falsch. Eine Möglichkeit, diese Schwierigkeit zu lösen,
besteht darin, dass wir zu einer gegebenen Interpretation
|| || eine Reihe anderer Interpretationen || ||', || ||'',
|| || ''', ... ableiten, die mit || || übereinstimmen
bis auf höchstens die Werte für eine Gegenstandskonstante
a. Diese Konstante kann durch die Folge der Interpretationen
|| ||', || ||'', || || ''', ... der Reihe nach auf alle Elemente
des Universums U abgebildet werden. Unter dieser
Voraussetzung kann die Semantik des Allquantors wie folgt
formalisiert werden: || ∀ Anmerkung 4.3.2 Diese Formalisierung ist adäquat:
Wir wollen nun definieren, was unter der Semantik der Prädikatenlogik zu verstehen ist. Die Semantik der Prädikatenlogik wird relativ zu einer Struktur
erklärt, wobei wir wieder die Interpretationsfunktion || ||M zur Bestimmung der Bedeutung eines prädikatenlogischen Satzes einführen werden. Die Interpretationsfunktion weist nun den Index M auf, um die Abhängigkeit der Interpretation von der Wahl der Strukur M anzuzeigen. Zunächst müssen wir angeben, wie Termausdrücke zu interpretieren sind: Definition 4.3.1 Die Interpretationsfunktion || ||M ist für Terme wie folgt definiert:
Wir erweitern nun || ||M auf Elemente der Menge PRAED: Definition 4.3.2 Eine Interpretation von PRAED über dem nicht-leeren Universum U ist gegeben durch || ||M, wobei gilt:
Anmerkung 4.3.3 Die Bedingung (4) aus
Definition 4.3.2 ist wesentlich. Sie besagt, dass der Satz
" Anmerkung 4.3.4 Die Einschränkung
der Interpretationsfunktion || ||M auf
Elemente p, q Die Begriffe der Tautologie, Erfüllbarkeit, Kontradiktion und Äquivalenz von Sätzen aus PRAED werden analog zu den korrespondierenden Begriffen der Aussagenlogik eingeführt. Insbesondere gilt also: Definition 4.3.3 Der semantische Ableitungsoperator
"
Anmerkung 4.3.5 Jeder aussagenlogisch wahre Satz ist gleichermaßen prädikatenlogisch wahr, da die Definition der prädikatenlogischen Interpretationsfunktion die Bestimmungen für aussagenlogische Bewertungen umfasst. Das Umgekehrte muss natürlich nicht gelten. Die selbe Überlegung gilt für aussagenlogisch gültige Schlüsse. Die Prädikatenlogik "enthält" also die Aussagenlogik. Definition 4.3.4 Sei M = < U,
R1, ..., Rn,
f1, ..., fm,
c1, ..., ck >
eine Struktur und seien p
Falls M Beispiel 4.3.2 Sei
falls || f || = +. Denn für alle || a
||, || b || Satz 4.3.1 Koinzidenztheorien: Sei
|| ||' Beweis: Wir beweisen das Koinzidenztheorem
induktiv über den Aufbau von A. Hierzu sei festgelegt,
dass der Grad einer Formel A gleich der Anzahl von
Symbolen aus {
Ganz analog verfährt man für den Fall, dass ||
∀ Das Koinzidenztheorem besagt intuitiv gesprochen, dass die Verschiedenheit der Interpretationen eines Satzes (d. h. etwa von || || und || ||') wesentlich von den Interpretationen der Konstanten des Satzes abhängt. Ein zweites Theorem, das wir hier nicht beweisen wollen, lautet: Satz 4.3.2 Überführungstheorem:
Gilt || ||' Mit anderen Worten: || ||' verhält sich wie || ||, nur im Falle von a existiert u. U. eine Abweichung beider Interpretationen, wobei hier || a ||' = || b || gilt. Mit diesen beiden Theoremen können wir nun folgende zwei Sätze beweisen: Satz 4.3.3 Alle Sätze der Gestalt
∀ Beweis: Wenn wir zeigen, dass aus der Falschheit
von ∀ Ist also || || eine beliebige Interpretation mit A
[a ] = 0, so gilt, falls b eine beliebige
Gegenstandskonstante ist, die in ∀ Wir benötigen in letzterem Beweis das Überführungstheorem,
da für || || nicht direkt die Richtigkeit eines quantifizierten
Ausdrucks gezeigt werden kann, sondern nur über eine
unendliche Menge von Interpretationen mit genannter Eigenschaft,
also insbesondere auch über || ||'. || ||' ist aber so
konstruiert, dass diese Interpretation in den Vordersatz ∀
Satz 4.3.4 Ist A Wir bemerken zunächst; A Beweis: Falls der Satz A Letzterer Satz besagt also, dass A Wir benötigen letztere beiden Sätze, um im folgenden die Prädikatenlogik kalkülisieren zu können.
|
| |
| In der Aussagenlogik haben wir mit der Methode der Wahrheitstabellen ein Entscheidungsverfahren für die Frage der Gültigkeit aussagenlogischer Formeln kennen gelernt. Für die PL existiert ein derart einfaches Verfahren nicht. Wir sind also ganz auf die Kalkülisierung der PL angewiesen. Den im folgenden vorzustellenden Kalkül nennen wir L. Er umfasst folgende Axiome und Ableitungsregeln: Definition 4.4.1 Die Menge AXIOM der Axiome der Prädikatenlogik enthält die folgenden Formeln aus SENT:
Anmerkung 4.4.1 Die ersten drei Axiome wiederholen exakt die Axiome aus Anmerkung 3.2.3. M. a. W.: Sämtliche in Definition 3.2.1 aufgeführten Axiome der Aussagenlogik gelten in gleicher Weise für die Prädikatenlogik. Definition 4.4.2 Im Kalkül L können zwei Deduktionsregeln verwendet werden:
Anmerkung 4.4.2 Die in der PL zum MP hinzutretende
Deduktionsregel ist selbstverständlich so zu lesen, dass
nur bei Geltung des Satzes A Wir beachten weiter, dass der Satz A Wir benutzen wieder den Ableitungsoperator Beispiel 4.4.1 Es gilt:
Denn:
Beispiel 4.4.2 Es gilt:
wobei a in
In der PL gilt das Deduktionstheorem nicht mit der Allgemeinheit
wie in der Aussagenlogik. Betrachten wir eine Interpretation
über der Menge { 0, 1 }. Sei || || eine Interpretation
mit | < a || = 0, || a' || = 1 sowie ||
F || = {< 0 >}. Es gilt dann || F ( a
) || = 1, hingegen gilt: || ∀ Satz 4.4.1 Falls P
Satz 4.4.2 Der Kalkül L der Prädikatenlogik ist widerspruchsfrei und vollständig. Beweis: Zur Widerspruchsfreiheit: Die Widerspruchsfreiheit der Axiome (1) bis (3) wurde bereits gezeigt. Axiom (a) ist mit Theorem 4.3.3 identisch, welches wir bereits bewiesen haben. Die Widerspruchsfreiheit des MP wurde ebenfalls schon für die Aussagenlogik gezeigt. Die Regel R2 entspricht wiederum Theorem 4.3.4, welches wir gleichermaßen bereits nachgewiesen haben.
|
| |
| Genauso wie in der Aussagenlogik lassen sich auch in der PL Normalformen von Sätzen dieser Sprache bilden. Die Bildung einer Normalform bedarf der Anwendung einer Reihe von Äquivalenzen. Für die hier besprochenen Normalformen werden dies vor allem die folgenden Äquivalenzen sein: Satz 4.5.1 Seien p, q
Es gilt aber:
Denn falls A das Prädikat "männlich" und B das Prädikat "weiblich" symbolisiert, und falls ferner als Referenzuniversum alle derzeit lebenden Menschen gewählt werden, dann lassen sich leicht Beispiele für das Behauptete konstruieren. Die Äquivalenzen aus Satz 4.5.1 "treiben" gewissermaßen, von links nach rechts angewandt, die Quantoren einer Formel nach "außen". Die Quantorenreihenfolge der Zielformel hängt dabei entscheidend von der Reihenfolge der Anwendung der Regeln ab. Sie ist also nicht eindeutig. Gleichartige Quantoren können aber immer vertauscht werden. Um die unter Punkt 2 der Satzes 4.5.1 genannten Äquivalenzen anwenden zu können, bedürfen wir unter Umständen der Möglichkeit einer Umbenennung von Variablen: Definition 4.5.1 Sei eine Formel p
Über die Ersetzung freier Variablen hinaus ist auch eine
"gebundene Umbenennung" möglich. Falls nämlich
F = Q x G eine Formel ist, wobei Q Satz 4.5.2 Eine Formel ist in Pränex-Normalform, falls sie von der Gestalt
ist, wobei Q Anmerkung 4.5.1 Die Pränex-Normalform läßt sich wieder algorithmisch herleiten. Hier die einzelnen Schritte:
Beispiel 4.5.1
≡
∀
≡ ∀ Für die Einführung der Skolem-Normalform benötigen wir noch folgende Definition: Definition 4.5.2 Eine Formel heißt bereinigt, falls keine Variable in dieser Formel gebunden als auch ungebunden vorkommt und weiterhin keine zwei Quantoren innerhalb der Formel dieselbe Variable quantifizieren. Es läßt sich zeigen, dass es zu jeder Formel eine äquivalente Formel in bereinigter Form gibt. Man hat nun die Definition Definition 4.5.3 Zu jeder prädikatenlogischen Formel p in Pränex-Normalform erhält man eine ihr zugehörige Formel in Skolem-Normalform (SNF) als das des folgenden Algorithmus: while p enthält eine Existenzquantor do
Satz 4.5.3 Für jede prädikatenlogische Formel p gilt: p ist erfüllbar iff die p entsprechende Skolem-Formel erfüllbar ist. Beweisidee: Der Algorithmus letzterer Definition ersetzt
systematisch jedes Vorkommen eines Existenzquantors in p.
Hierbei erhält man durch jeden dieser Schritte eine Formel,
die wir p' nennen wollen. Für jede solche Formel
p' zeigt man allgemein, dass gilt: p ist erfüllbar
iff p' erfüllbar ist. Dies erreicht man im wesentlichen
dadurch, dass man für die Funktion || f || über
dem Referenzuniversum festlegt, dass || f || ( u1,
..., un = v, mit || yj
|| = uj für j Letzterer Satz besagt also, dass die Erfüllbarkeitseigenschaft einer Formel gleichermaßen an der ihr entsprechenden Formel in SNF beobachtet werden kann. Wir wollen nun von einer beliebigen prädikatenlogischen Formel p ausgehen (eventuell auch mit Vorkommen freier Variablen) und die Schritte betrachten, die diese durchlaufen muss, um zu ihrer SNF zu gelangen:
Beispiel 4.5.2 Sei
p ist nicht bereinigt: y wird an zwei verschiedenen Stellen gebunden. Also: Substitution von y durch w im zweiten Disjunktionsglied:
Die Variable z kommt in p1 frei vor. Also bildet man:
Umformen in Pränex-NF liefert:
Wir erhalten nun eine zu p3 korrespondierende Formel in SNF, indem wir eine nullstellige Funktion a (das heißt eine Gegenstandskonstante) für z sowie h ( x ) für y substituieren:
Die Formel p5 läßt sich, wie wir sehen werden, unmittelbar in die sog. Klauselform übertragen, die für die Resolution unabdingbar ist. |
|
|
 " (Allquantor) und "
" (Allquantor) und " 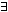 " (Existenzquantor). Sei P ein einstelliges Prädikat,
dann lassen sich die Aussagen "Für alle Entitäten
des betrachteten Universums U gilt P"
und "Es existiert eine Entität im Universum mit der
Eigenschaft P" formalisieren sich zu " ∀
" (Existenzquantor). Sei P ein einstelliges Prädikat,
dann lassen sich die Aussagen "Für alle Entitäten
des betrachteten Universums U gilt P"
und "Es existiert eine Entität im Universum mit der
Eigenschaft P" formalisieren sich zu " ∀
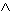 G (
x, y ))
G (
x, y )) 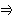 P (
x ) " bezieht sich der Quantor nicht auf die dritte
Okkurenz von x. Ferner gilt, dass Quantoren stärker
binden als die logischen Funktoren "
P (
x ) " bezieht sich der Quantor nicht auf die dritte
Okkurenz von x. Ferner gilt, dass Quantoren stärker
binden als die logischen Funktoren " 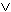 , etc. Die Ersetzung einer Konstanten durch
eine Variable, die anschließend durch einen Quantor gebunden
wird, nennt man Quantifizierung.
, etc. Die Ersetzung einer Konstanten durch
eine Variable, die anschließend durch einen Quantor gebunden
wird, nennt man Quantifizierung. ∀
∀ TERM,
TERM, TERM
und f
TERM
und f 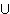 FV ( q ),
FV ( q ),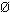 . SENT = {
p
. SENT = {
p 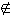 || G ||. Es ist
nun || F ( a, a'' ) || = 1 iff
das Zahlenpaar < || a ||, || a'' ||
>
|| G ||. Es ist
nun || F ( a, a'' ) || = 1 iff
das Zahlenpaar < || a ||, || a'' ||
>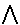
 p iff || p ||M = 1.
p iff || p ||M = 1. Hat A die Gestalt ¬
p, p
Hat A die Gestalt ¬
p, p 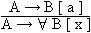
 q im Kalkül L
beweisbar ist, dann auch P
q im Kalkül L
beweisbar ist, dann auch P